1. 比特位计数 + n&(n-1)的妙用

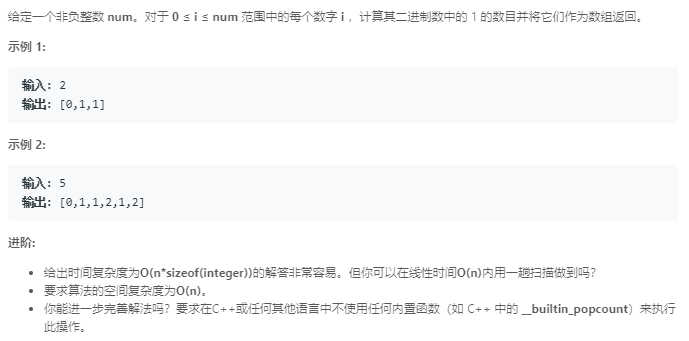
• 题目

  

• 解析

  0   0000
  1   0001
  2   0010 
  3   0011
  4   0100
  5   0101
  6   0110
  7   0111
  8   1000
  9   1001
  10  1010
  11  1011
  12  1100
  13  1101
  14  1110
  15  1111

1. 假设求r[i]
2. r[i - 1] + 1 ，如果进位，那么r[i]就和r[i - 1] 没有关系了，如果没有进位，那么，r[i] = r[i - 1] + 1
3. 接着，看进位的情况：如果 i & (i - 1) ，那么就会把i和 i - 1 的最低位去掉，即变为0；
   

   Ps: 最低位是指，从左面第0位开始，一直往右数，直到遇到两个数不一样的位置，那么后面的数（包括不一样的数）不管相不相同，都为最低位（例：9 和 10：从左面第0位开始，到第2位不同，那么第2、3位即为最低位）

4. 显而易见，i & (i - 1)得到的数就是去掉最低位之后的数，那么，由于进位了，所以，r[i] = r[i & (i - 1)] + 1

• 代码

vector<int> countBits(int num) {
    vector<int> r(num + 1);
    r[0] = 0;
    for(int i = 1; i <= num; i++) {
        r[i] = r[i & (i - 1)] + 1;
    }
    return r;
}

---

• n&(n-1)的妙用

1. 判断一个数是否是2的方幂

1. 方法：n > 0 && ((n & (n - 1)) == 0 )

2. 解释：
   ((n & (n-1)) == 0)：

   如果A&B==0，表示A与B的二进制形式没有在同一个位置都为1的时候。

   不妨先看下n-1是什么意思。

   令:n=1101011000(二进制,十进制也一样)，则

   n-1=1101010111。

   n&(n-1)=1101010000

   由此可以得出，n和n-1的低位不一样，直到有个转折点，就是借位的那个点，从这个点开始的高位，n和n-1都一样，如果高位一样这就造成一个问题，就是n和n-1在相同的位上可能会有同一个1，从而使((n & (n-1)) != 0),如果想要((n & (n-1)) == 0)，则高位必须全为0，这样就没有相同的1。

   所以n是2的幂或0

2. 求某一个数的二进制表示中1的个数

while (n >0 ) {
      count ++;
      n &= (n-1);
}

3. 计算N!的质因数2的个数

1. N!质因数2的个数 = [N / 2] + [N / 4] + [N / 8] + ….

2. 过程：
   下面通过一个简单的例子来推导一下过程：N = 10101(二进制表示）

   现在我们跟踪最高位的1，不考虑其他位假定为0，

   则在

   [N / 2]    01000
   
   [N / 4]    00100
   
   [N / 8]    00010
   
   [N / 8]    00001
   
   则所有相加等于01111 = 10000 - 1

   由此推及其他位可得：(10101)!的质因数2的个数为10000 - 1 + 00100 - 1 + 00001 - 1 = 10101 - 3(二进制表示中1的个数)

   推及一般N!的质因数2的个数为N - （N二进制表示中1的个数）

   n&(-n)在树状数组中lowbit出现   用来求 t 中的因子中形如2^k的数为多少     用来取得n最右边的1，可以知道其因子中有几个2

   10:  0000 1010

   -10: 1111 0110

   10&(-10)为 0010  =  2  所以10的因子中为2的有一个，2^k的形式的为2^1

   8&(-8) = [1000] = 8   所以8的因子中为2的有3个，2^k的形式为2^3